크루스칼 알고리즘(Kruskal Algorithm), 최소 신장 트리(MST)

• 모든 정점을 포함하고 사이클이 없는 연결 선을 그릴 때, 가중치의 합이 최소가 되는 상황에 사용

신장 트리(Spanning Tree)

• 모든 정점(vertex)이 연결
• 정점 간 서로 연결이되고, 싸이클이 존재하지 않는 그래프
• n개의 정점을 모두 연결할 수 있는 n-1개의 엣지로 이루어진 부분 그래프

최소 신장 트리(Minimum Spanning Tree, MST)

• 신장 트리 집합 중 가중치의 합이 최소가 되는 신장 트리

-> 크루스칼 알고리즘은 최소 신장 트리를 구할 때 사용

크루스칼 알고리즘(Kruskal Algorithm)

• 그리디 알고리즘의 일종
• 그래프의 간선들을 가중치의 오름차순으로 정렬
• 사이클이 형성되지 않으면서 정렬된 순서로 간선을 선택

사이클 판단하기 - Union & Find

• Disjoint Set(서로소 집합)을 표현하는 자료구조
• 서로 다른 두 집합을 병합하는 Union 연산
• 집합 원소가 어떤 집합에 속해있는지를 찾는 Find 연산

# 크루스칼 알고리즘
# vertex가 어떤 집합에 속해있는지 찾아줌 
def find(parent,vertex):
    if parent[vertex] != vertex:
            parent[vertex] = find(parent,parent[vertex])
    return parent[vertex]
# vertex a와 b를 같은 집합으로 합쳐줌, a와 b의 집합 중 더 작은 값이 그룹을 나타냄
def union(parent,a,b):
    a = find(parent,a)
    b = find(parent,b)
    if a<b:
        parent[b]=a
    else:
        parent[a]=b
def solution(n,weights):
    answer=0
    weights.sort(가중치에 대한 오름차순 정렬)
    parent=[i for i in range(n)]
    # edge
    for edge in edges:
        # edge 표현 start-end-weight
        start,end,weight
        # start-end의 집합 확인
        a = find(parent,start)
        b = find(parent,end)
        # a와 b가 다른 집합이면 union(싸이클 생성x)
        if a!=b:
            union(parent,a,b)
            answer+=weight
    return answer

예제)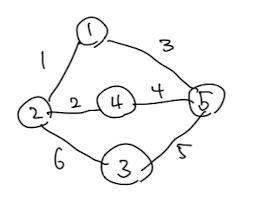

1. 간선들을 가중치에 따라 정렬, 어떤 집합에 속해있는지에 대한 배열(초기에는 자기 자신)

• 가중치에 따라 정렬된 가중치 배열
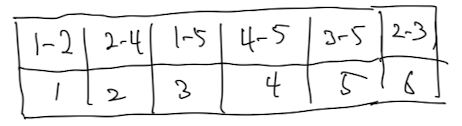
• 어떤 집합에 속해 있는지 나타내는 parent 배열

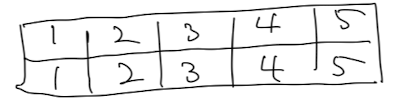
2. 가중치 배열에 따라 싸이클이 생기지 않도록 간선 선택
   a. 노드 1과 2의 parent가 다르므로 간선 1-2 추가, 노드 2의 parent -> 1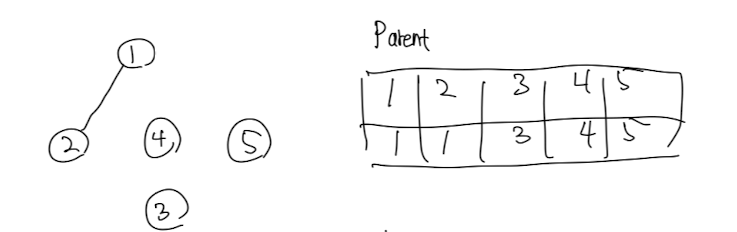
   b. 노드 2와 4의 parent가 다르므로 간선 2-4 추가, 4의 parent -> 1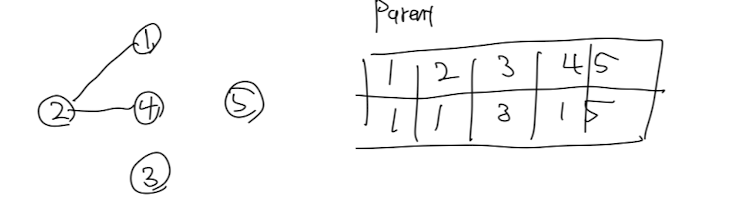
   c. 노드 1과 5의 parent가 다르므로 간선 1-5 추가 5의 parent ->1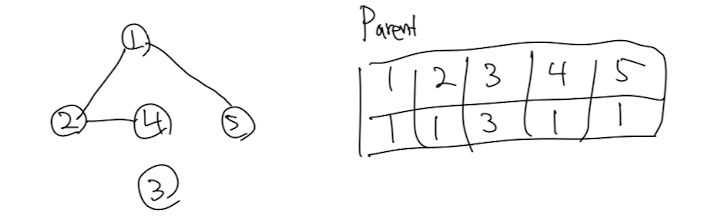 d. 노드 4와 5의 parent는 같으므로 간선 4-5는 추가하지 않는다.
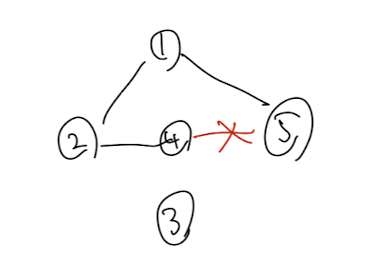   e. 노드 3과 5의 parent가 다르므로 간선 3-5 추가

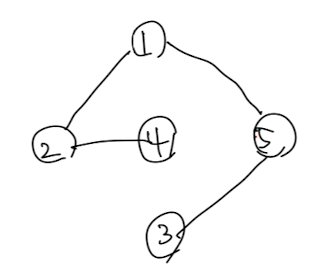
-> 5개의 정점이 4개의 간선으로 모두 연결된 최소 신장 트리